What Sparse Light Field Coding Reveals about Scene Structure

Ole Johannsen, Antonin Sulc, and Bastian Goldluecke

Contribution

Sparse coding scheme for accurate light field depth estimation with multiple depth layers Idea: explain EPI patches as sparse linear combinations of atoms with known disparity:

  • estimate set of lower dimensional generators from center view
  • lift each generator element to EPI space according to a set of disparities
  • sparsely encode every EPI patch with the resulting set of atoms
  • analyze sparse coding coefficients to estimate final patch disparities
Applications  
  • Robust depth estimation
  • Depth estimation of multiple layers with different depth                                                               

Light fields and epipolar plane images (EPIs)

Light field: regular grid of views, identical cameras with parallel optical axes, parametrized with view coordinates (s, t) and image coordinates (x, y).
2D EPIs: horizontal slices with fixed (x, s) or vertical slices with fixed (t, y). Projection of a 3D point: line on an EPI, whose orientation corresponds to disparity.
Superimposed layers (reflections or tranparent objects): two super-imposed orientations.

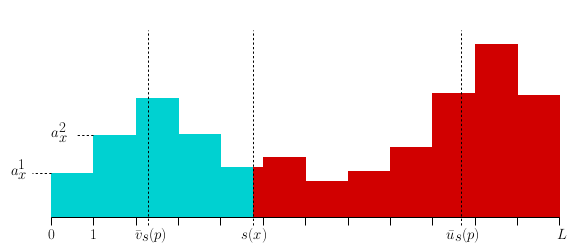
Dictionary construction

Key idea: each atom corresponds to a unique disparity

Generators (blue)

Generators are patches in the center view, obtained from dictionary learning or PCA.
Choice of different formats: 1D, crosshair and 2D patches, resulting in 2D and 4D dictionary
elements. In our experience, 1D generators (i.e. 2D atoms) work best.

Dictionary atoms (red)
The Generators are shifted according to a discrete set of disparities. The generators are
larger than the atoms - i.e. the shifted generator (yellow) must be cropped to yield the final
atom (red).

The complete dictionary D

For each combination of disparity label and generator we generate one dictionary element.

Sparse coding for disparity estimation

Each EPI patch is encoded as a sparse linear combination of the atoms,

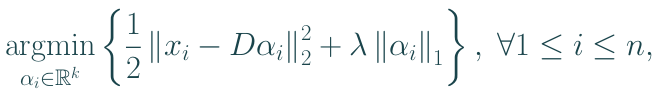
Idea: analysis of the coefficient distribution should give information about depth layers.

Lambertian surfaces: one disparity layer

Sparse coding coefficents are pooled into groups with the same disparity. A single Gaussian is
fitted to the data, after which we perform variational smoothing on the mean values, weighted
with the standard deviation of the Gaussian.

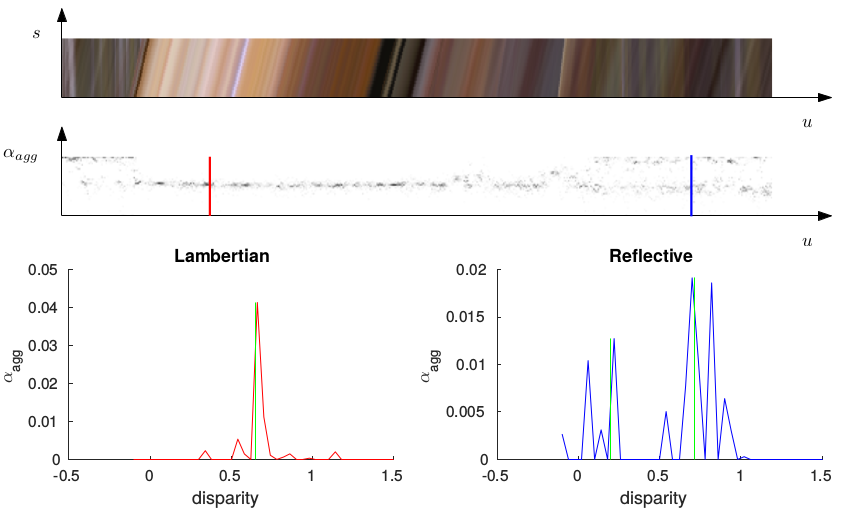
We also use a statistical test for two-peakedness of a distribution, and embed the score
into a binary segmentation problem to obtain a mask for possible two-layered regions.

Twin peaks: two disparity layers

In the candidate regions for the presence of two layers, we fit a two-component GMM to
the distribution of coefficients. Starting from the two means and their midpoint, we iteratively
optimise over the separation point and the two disparities in a variational framework.

This work was supported by the ERC Starting Grant ”Light Field Imaging and Analysis” (LIA 336978, FP7-2014).
Presented at the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, June 2016.